mlx_optimizers.ADOPT

Contents

mlx_optimizers.ADOPT#

class ADOPT(learning_rate: float | ~typing.Callable[[~mlx.core.array], ~mlx.core.array], betas: ~typing.List[float] = [0.9, 0.9999], weight_decay: float = 0.0, decouple: bool = False, clip_lambda: ~typing.Callable[[~mlx.core.array], ~mlx.core.array] | None = <function ADOPT.<lambda>>, eps: float = 1e-06)#

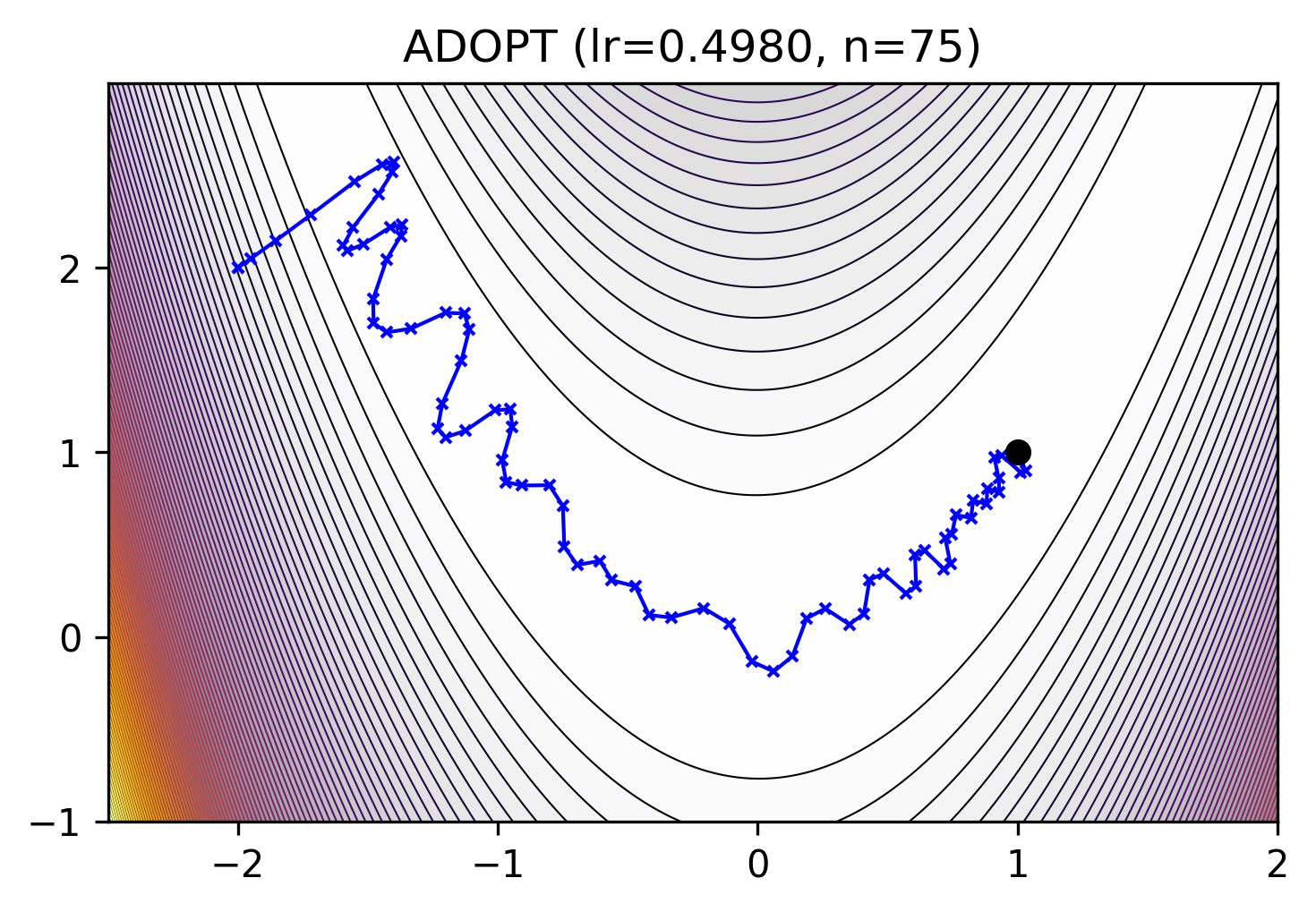
ADaptive gradient method with the OPTimal convergence rate [1].

\[\begin{split}m_0 &= \mathbf{0}, \quad v_0 = g_0^2 \\ m_t &= \beta_1 m_{t-1} + (1 - \beta_1) \text{clip} \left( \frac{g_t}{\text{max}(\sqrt{v_{t-1}, \epsilon})}, c_t\right) \\ \theta_{t} &= \theta_{t-1} - \eta m_t \\ v_{t} &= \beta_2 v_{t-1} + (1 - \beta_2) g_t^2\end{split}\]

[1] Taniguchi, Shohei, et al., 2024. ADOPT: Modified Adam Can Converge with Any \(\beta_2\) with the Optimal Rate. NeurIPS 2024. https://arxiv.org/abs/2411.02853 iShohei220/adopt

Parameters:

  • learning_rate (float or callable) – The learning rate \(\eta\).

  • betas (List[float, float], optional) – The coefficients \((\beta_1, \beta_2)\) used for computing running averages of the gradient and its square. Default: (0.9, 0.9999)

  • weight_decay (float, optional) – The weight decay. Default: 0.0

  • decouple (bool, optional) – AdamW if True. Default: False

  • clip_lambda (callable, optional) – The clipping function \(c_t\) for the gradient. Set to None for previous behavior. Default: step**0.25

  • eps (float, optional) – The term \(\epsilon\) added to the denominator to improve numerical stability. Default: 1e-6

../_images/rosenbrock_ADOPT.png

Methods

__init__(learning_rate[, betas, ...])

apply_single(gradient, parameter, state)

Performs a single optimization step, updating \(m\) and \(v\)

init_single(parameter, state)

Initialize optimizer state
Contents